1. What is Congruence? (Ek Jaise Judwa)
Congruence ka simple matlab hai: Sab kuch same — Size bhi aur Shape bhi.
Agar main ek shape ko utha kar dusre ke upar rakhun, aur wo use pura cover kar le (na chota, na bada), toh wo Congruent hain.
Ek Parle-G ka packet kholo. Usme se 2 biscuits nikalo.
Kya wo dikhne mein same hain? Haan!
Kya ek biscuit dusre ko pura dhak (cover) leta hai? Haan!
Bas yehi Congruence hai. Maths mein hum shape aur size dekhte hain, taste nahi! 😉
2. Congruence Rules (Kaise check karein?)
Har baar triangles ko kaat kar ek dusre ke upar rakhna possible nahi hai. Isliye hum kuch Rules use karte hain.
rule 1: SAS (Side-Angle-Side)
Agar ek triangle ki 2 Sides aur unke beech ka Included Angle dusre triangle ke barabar ho, toh wo Congruent hain.
Think of it as a "V" shape jiske arms fixed length ke hain aur unke beech ka angle fixed hai.
Example:
Triangle ABC aur Triangle PQR mein:
- AB = PQ = 5cm
- AC = PR = 7cm
- Angle A = Angle P = 50°
Dono taraf SAS rule lag raha hai, isliye ΔABC ≅ ΔPQR.
rule 2: ASA (Angle-Side-Angle)
Agar 2 Angles aur unke beech ki Included Side barabar ho.
Real Life Example:
Do bridges (pul) imagine karo. Agar dono ki choudai (width/side) same hai aur dono taraf ke poles ka angle same hai, toh pura bridge identical banega.
Theorem (ASA): Two triangles are congruent if two angles and included side are equal.
Logic for Proof:
Hum maante hain ki ΔABC aur ΔDEF hain jahan angle B=E, C=F, aur Side BC=EF.
- Case 1: Maan lo AB = DE. Phir toh SAS rule se dono congruent ho gaye. Proof Done.
- Case 2: Maan lo AB > DE. Agar hum isko zabardasti congruent karne ki koshish karenge, toh hume pata chalega ki ye impossible hai (Contradiction).
Iska matlab sirf Case 1 hi sach ho sakta hai: Sizes barabar honi hi padengi.
rule 3: SSS (Side-Side-Side)
Agar teeno sides barabar hain, toh triangle congruent hoga. Triangle shape ki yehi khasiyat hai — ye "Rigid" hota hai.
Why Bridges Use Triangles?
Kyunki SSS rule ki wajah se Triangles kabhi apna shape change nahi karte (dabte nahi hain). Squares dab kar Rhombus ban sakte hain, par Triangle triangle hi rehta hai.
rule 4: RHS (Right Angle - Hypotenuse - Side)
Ye rule sirf Right-Angled Triangles (90°) ke liye hai.
Agar Hypotenuse aur koi ek Side barabar ho, toh triangles congruent honge.
Ladder Example:
Ek seedhi deewar (90°). Ek seedhi (Length) jo deewar pe lagi hai. Agar seedhi ki lambai (Hypotenuse) aur deewar se duri (Side) fix kar do, toh seedhi hamesha wahi height tak pahunchegi.
📊 Visual Summary: Congruence Rules
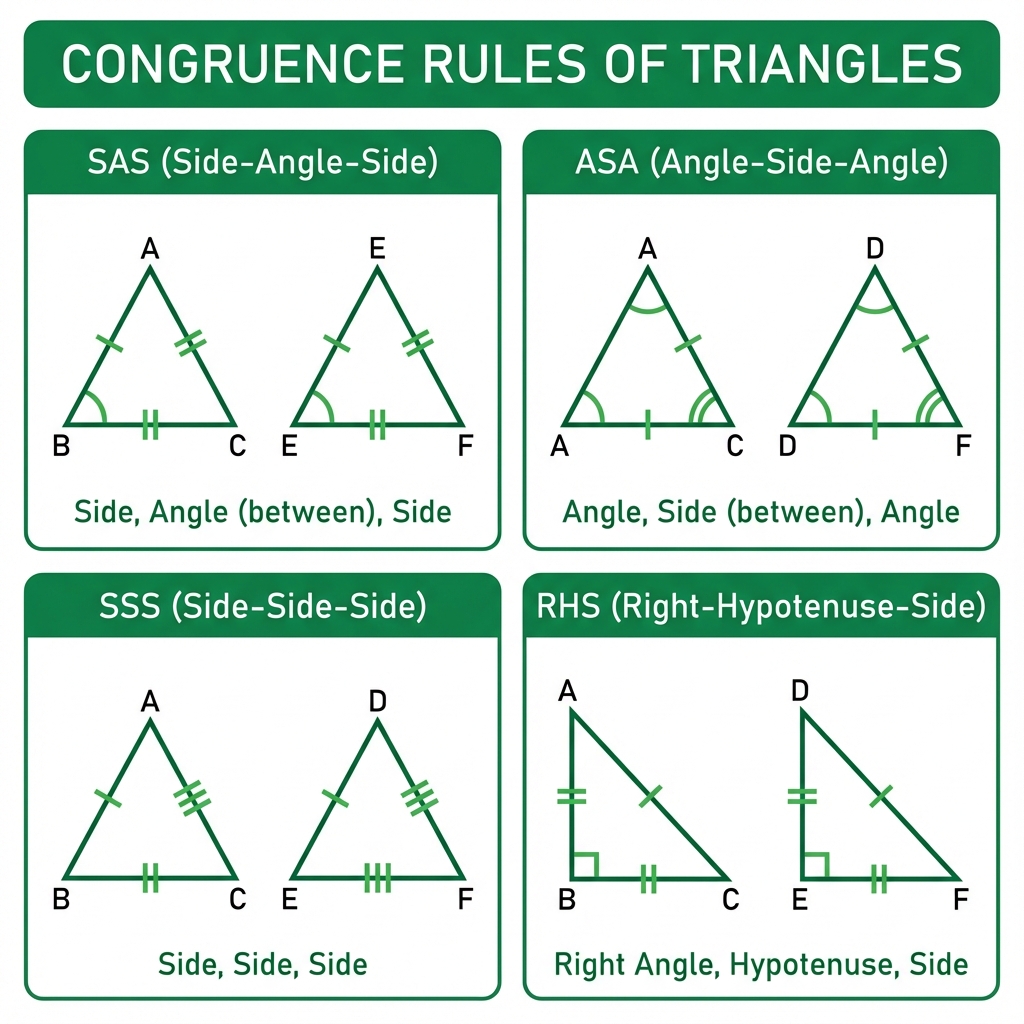
3. Isosceles Triangle Properties
Isosceles (Samdvibahu) Triangle wo hota hai jiski 2 sides equal hoti hain.
Theorem: Angles opposite to equal sides of an isosceles triangle are equal.
Proof (Saboot):
Hume diya hai: AB = AC. Prove karna hai: Angle B = Angle C.
- Hum ek line AD banayenge jo Angle A ko aadha baant-te hue (bisect) neeche aaye.
- Ab do naye triangles dekho: ΔABD aur ΔACD.
- AB = AC (Diya hai)
- Angle BAD = Angle CAD (Humne bisector banaya)
- AD = AD (Common side)
So, ΔABD ≅ ΔACD (By SAS Rule).
Iska matlab unke saare parts barabar honge (CPCT - Corresponding Parts of Congruent Triangles).
So, Angle B = Angle C. (Proved!)
Triangle PQR mein PQ = PR hai. Agar Angle Q = 50° hai, toh Angle R kya hoga?
Answer: Since sides equal hain, toh opposite angles bhi equal honge. So, Angle R bhi 50° hoga.
📌 Aage Ka Content (Next Chapter)
Triangles ke rules clear hain? Ab hum in rules ko use karke 4-sided figures (Quadrilaterals) ko samjhenge.